 Heron de Alexandria foi um matemático Grego do século I por volta do ano 62.
Heron de Alexandria foi um matemático Grego do século I por volta do ano 62.
Ele ficou conhecido pelo desenvolvimento da fórmula que leva seu nome, o Teorema de Herão (ou Heron) que nos permite calcular a área de um triângulo qualquer à partir dos seus lados.
Já estamos acostumados a calcularmos a área de um triângulo utilizando a fórmula da base vezes altura dividida por dois, mas o Teorema de Herão nos permite calcular área de triângulos sem precisarmos saber necessariamente a base a altura do mesmo, o que pode ser muito mais rápido e útil em alguns casos.
Com o Teorema de Herão é possível também determinar, por exemplo o raio de uma circunferência inscrita num triângulo, através da área do triângulo e seu semiperímetro.
A fórmula:
A fórmula do Teorema de Herão nos permite calcular a área de qualquer triângulo, para isto basta conhecer seus três lados, como já mencionado.
A fórmula é a seguinte:
![A= \,\sqrt[]{s\,(s-a)(s-b)(s-c)}](http://www.ajudamatematica.com/latexrender/pictures/1f145efa43e3c981af009b05e96b5a2e.png)
Onde A é a área do triângulo, s representa o semiperímetro do mesmo, e a,b e c são os lados do triângulo.
O perímetro de um triângulo se dá pela soma de seus três lados, logo, seu semiperímetro é a metade do perímetro, ou seja, o perímetro divido por 2.
Vamos ver um exemplo?
Num triângulo ABC, cujo lados são 5, 12 e 13 cm, calcule a sua área.

Pois bem, nós conhecemos os três lados do triângulo: 13, 12 e 5 cm.
Para encontramos o perímetro do mesmo, basta somar seus lados:
P = 13 + 5 + 12
P = 30
Se o perímetro deste triângulo é igual à 30 cm, seu semiperímetro será o perímetro divido por dois (a metade), logo o semiperímetro deste triângulo é igual à 15 cm, pois: 30/2 = 15
Então aplicamos esses números na fórmula, teremos:
Faça o que há dentro dos parênteses primeiro:
Faça a multiplicação de tudo e obtenha:
A raiz quadrada de 900 é igual à 30, logo, a área deste triângulo mede 30 cm²:
Circunferência Inscrita no triângulo:
E se uma circunferência estiver inscrita num triângulo com os mesmos lados que o triângulo anterior, qual seria o raio dela?
Então se este triângulo possui os mesmos lados que o triângulo anterior, então esses lados são de 13, 12 e 5 cm.
Para determinarmos o raio da circunferência inscrita neste triângulo, basta aplicarmos a seguinte fórmula:
A é a área do triângulo, S é o semiperímetro do mesmo e r é o raio da circunferência que é o que queremos encontrar.
Se este triângulo tem os mesmos lados que o anterior, então nós já temos as medidas da área e do semiperímetro dele, lembra? O semiperímetro deste triângulo é igual à 15 cm e a área é igual à 30 cm².
Aplicando os números na fórmula temos:
Isole r e tenha:
30 dividido por 15 dará 2, logo o raio da circunferência inscrita neste triângulo de área igual à 30 cm² é igual à 2 cm.
Outro exemplo?
Um triângulo de vértices ABC circunscrito numa circunferência possui AB = 5 cm, AC= 7 cm, cujo ângulo  é igual à 82 graus. Calcule BC e descubra o raio da circunferência e a sua área.
Então aí está nosso triângulo e nossa circunferência!
Para descobrirmos o raio da circunferência e consequentemente sua área, primeiro precisamos do valor da área total do triângulo, que por sua vez só pode ser encontrada através do Teorema de Herão.
Mas para o Teorema de Herão dar certo, precisamos saber os três lados do triângulo, e aqui nós sabemos apenas dois. Como podemos encontrar o terceiro lado? Isso te faz lembrar de algo? Algo como a Lei dos Cossenos? Sim! Vamos utilizar a lei dos Cossenos para encontrarmos o terceiro lado deste triângulo.
Veja nosso triângulo aqui, sem estar circunscrito na circunferência:
Relacionando os lados com os ângulos do triângulo, podemos afirmar que o lado b é igual à 7 cm, o lado c é igual à 5 cm e o lado a é x, por estar oposto ao ângulo Â. Sabemos também quem é o ângulo Â, logo, nossa fórmula da lei dos cossenos será em função ao ângulo Â:
a² = b² + c² - 2.b.c. cos Â
Substituindo os números na fórmula:
a² = 7² + 5² - 2. 7. 5. cos 82°
a² = 49 + 25 - 70. cos 82°
a² = 74 - 70. cos 82°
Verifique na tabela trigonométrica o cosseno de 82 graus e descubra que é igual à aproximadamente 0,13. Logo, teremos 70 * 0,13 = 9,1
a² = 74 - 9,1
a² = 64,9
a = √64,9
a = aproximadamente 8
Então nosso terceiro lado é igual à 8 cm:
Então agora que sabemos os três lados do triângulo, podemos utilizar o Teorema de Herão:
Encontrando o perímetro do triângulo:
P = 8 + 7 + 5
P = 20
Então o semiperímetro do triângulo é 10 -> 20/2 = 10
Substituindo os valores na fórmula:
Então agora sabemos a área do triângulo e o semiperímetro do mesmo, basta agora aplicarmos na fórmula para encontrarmos o raio da circunferência:
Então o raio da circunferência é igual à 1,73 cm.
O problema nos pede também para calcularmos a área da circunferência inscrita no triângulo. Você se lembra da fórmula para encontrar a área de um círculo?
Então:
Então a área dessa circunferência inscrita no triângulo é igual à aproximadamente 3 pi.
Ou se você considerar pi = 3,14 a área será de: 9,40 cm² aproximadamente.
Resolução: O lado BC do triângulo é igual à 8 cm, e o raio da circunferência inscrita no mesmo é de 1,73 cm e a área da mesma é igual à aproximadamente 9,40 cm².
 Heron de Alexandria foi um matemático Grego do século I por volta do ano 62.
Heron de Alexandria foi um matemático Grego do século I por volta do ano 62.![A= \,\sqrt[]{s\,(s-a)(s-b)(s-c)}](http://www.ajudamatematica.com/latexrender/pictures/1f145efa43e3c981af009b05e96b5a2e.png)
![A= \,\sqrt[]{15\,(15-13)(15-12)(15-5)}](http://www.ajudamatematica.com/latexrender/pictures/99da7f28ba08051196d07cfd855679ef.png)
![A= \,\sqrt[]{15*\,2*\,3*\,10}](http://www.ajudamatematica.com/latexrender/pictures/a8a9c20769360ce6aec84fce75724575.png)
![A= \,\sqrt[]{900}](http://www.ajudamatematica.com/latexrender/pictures/a51bee143daad34ddcf7432191c67b7c.png)



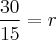
![A= \,\sqrt[]{s\,(s-a)(s-b)(s-c)}](http://www.ajudamatematica.com/latexrender/pictures/1f145efa43e3c981af009b05e96b5a2e.png)
![A= \,\sqrt[]{10\,(10-8)(10-7)(10-5)}](http://www.ajudamatematica.com/latexrender/pictures/e098df6412a3edbe246c8d333da4e6f1.png)
![A= \,\sqrt[]{10\, * 2 * 3 * 5}](http://www.ajudamatematica.com/latexrender/pictures/ebe89874a6136dcc1bfc1f6289607779.png)
![A= \,\sqrt[]{300}](http://www.ajudamatematica.com/latexrender/pictures/8ff21389835c86a774e35b961c2dee6d.png)
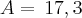

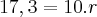
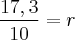

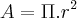
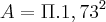
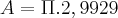







0 comentários:
Postar um comentário