Logaritimos: Conceitos Iniciais ~ Aulas da May

Introdução:
Hoje vamos ficar de frente com um assunto muito importante e muito estudado na matemática: O Logaritmo. Porém, antes de querer aprender sobre logaritmos, você deve ter uma boa noção sobre fatoração, potenciação, raízes e equações exponencias! Se você já domina bem esses assuntos, acompanhe a aula à seguir, do contrário, acesse os links indicados acima e estude-os antes de querer aprender logaritmo, certo?
Vamos lá...

A História do Logaritmo:
Os logaritmos foram criados para facilitar cálculos complexos relacionados à astronomia e navegação, transformando grandes e complexas operações de multiplicação em somas, e divisões em subtrações.
Os logaritmos foram criados pelos matemáticos: John Napier que era escocês e Jobst Bürgi que era suíço, por volta do século XVII.
Graças aos logaritmos, cálculos muito complexos poderiam ser realizados com mais facilidade, e nessa época, onde não existiam máquinas de calcular nem nada do tipo que facilitasse tais cálculos, os logaritmos foram um avanço e tanto!
Apesar disso, os logaritmos desenvolvidos por Napier se utilizavam de bases não exatas, foi então que Henry Briggs sugeriu à Napier para que se introduzisse aos logaritmos, bases decimais ao invés dessas bases não exatas.
Foi daí que surgiram os logaritmos decimais, e mais tarde a tábua logarítmica, que mostrava os logaritmos de qualquer número numa base decimal.
Hoje em dia não é necessário utilizarmos essa tábua, por existirem as calculadoras científicas, mas no século dezessete, essa tábua era de grande ajuda, assim como os logaritmos são até hoje.

Definição de Logaritmo:
O logaritmo é uma operação matemática que pode facilitar cálculos muito complexos envolvendo potências e consequentemente equações exponenciais.
Veja um exemplo de logaritmo simples:
Você saberia me dizer quanto é 3 ao quadrado? 3²?
3² = 3.3 = 9, certo? Certo! Isso a gente vê em potenciação! Mas e se acontecesse de termos algo como isto:

${3}^{x}\,=\,9$

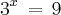
O que isso indica? Indica que queremos saber qual número que elevado à base 3 dará 9.
Mas isso a gente já viu acima, certo? Três ao quadrado dá nove, ou seja, o número que elevado à base 3 que dará nove é o dois: 3² = 9
Mas a gente pode escrever isso da seguinte maneira:

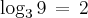
$\log_{3} 9\,=\,2$

Isso significa que o número dois é o logaritmo de nove na base 3.
Para lembrar disso pense da seguinte forma: ''Que número elevado à base 3 dará nove?'' Esse número é o logaritmo, ou como conhecido em potenciação, o expoente!
Vamos ver mais um exemplo?
Que número elevado à base 2 dará 16?

${2}^{x} = 16$

Ué, isso você viu em equação exponencial! Para resolver um problema desses basta igualar as bases fatorando uma delas para encontrar o valor de x. No caso, o 16 está em mais condições de ser fatorado até o 2, então:

16|2
8 |2
4 |2
2 |2
1

Então temos:

${2}^{x} = {2}^{4}$

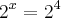
Agora basta a gente cancelar as bases iguais, e ficaremos com x = 4
Logo, o número que elevado à base 2 que dará 16 é o 4.
Ou em outras palavras, podemos dizer que 4 é o logaritmo de 16 na base 2.
Podemos escrever isso assim:

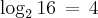
$\log_{2} 16\,=\,4$

Outro exemplo? Você sabe me dizer qual o logaritmo de 64 na base 2?

$\log_{2} 64\,=\,x$

Vamos ver?
Você poderia fazer isso de cabeça, mas vamos realizar a operação para não restar nenhuma dúvida:

$\log_{2} 64\,=\,x$

Lembre-se da pergunta a ser feita a si mesmo: "Que número que é elevado à base 2 que dará 64?''
Vamos escrever isso numa equação?

${2}^{x}\,=\,64$

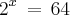
Então caímos na equação exponencial! Vamos resolver?
Primeiro passo: Fatorar uma das bases para igualá-las. Vamos fatorar o 64:
64 |2
32 |2
16 |2
8 |2
4 |2
2 |2
1

Então temos:

${2}^{x}\,=\, {2}^{6}$

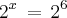
Cancelando as bases iguais temos x= 6
Ou seja, o logaritmo de 64 na base 2 é igual é 6.

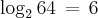
$\log_{2} 64\,=\,6$

Sabendo bem disso, segue aqui a definição de logaritmo, onde:

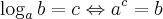
$\log_{a}b = c \Leftrightarrow {a}^{c} = b$

Isso quer dizer que: O logaritmo de B na base A é igual à C, ou seja, C elevado à base A dará B.
Você já viu a definição de logaritmo (log) na prática, logo acima, veja:

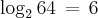
$\log_{2} 64\,=\,6$

6 é o logaritmo de 64 na base 2, ou seja, 2 elevado à 6 dará 64.
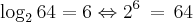
$\log_{2}64 = 6 \Leftrightarrow {2}^{6}\,=\,64$

Nomenclaturas:
Segundo a definição:

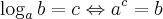
$\log_{a}b = c \Leftrightarrow {a}^{c} = b$

Podemos dizer que o ''a'' chama-se base, o ''b'' chama-se logaritmando, e ''c'' é o resultado da operação, ou seja o próprio logaritmo. Exemplo?

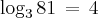
$\log_{3} 81\,=\,4$

Aqui podemos chamar o três de base, o 81 de logaritmando e o quatro de logaritmo.

Condições de existência:
Algo a ser observado e lembrado também, são as condições de existência de um logaritmo que são:

a > 0
a ≠ 1
b > 0

Ou seja, a base (''a'') deve ser um número positivo e diferente de 1, assim como o logaritmando (''b''), que apenas deve ser um número positivo.
Ou seja, não podemos ter a base de um logaritmo sendo um número negativo nem sendo 1, assim como não podemos ter um logaritmando negativo.

Alguns exercícios simples:
Bem, agora que você sabe algumas informações básicas, vamos aprender a resolver um logaritmo? Veja alguns exemplos abaixo, e se atente à resolução deles:

$\log_{5} 125$

Aqui vamos encontrar o logaritmo de 125 na base 5.
Primeiro, vamos seguir a definição dos logaritmos e vamos criar a seguinte equação:

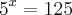
${5}^{x} = 125$

Agora vamos tentar fatorar o 125 até o 5 para igualarmos as bases:

125 | 5
25 | 5
5 | 5
1

Logo temos:

${5}^{x} = {5}^{3}$

Cancelando as bases temos: x= 3
Então o Log de 125 na base 5 é 3.

$\log_{5} 125 = 3$

E esse?

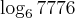
$\log_{6}7776$

Vamos criar a equação:

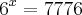
${6}^{x} = 7776$

Decompondo o 7776:

7776 | 2
3888 | 2
1944 | 2
972 | 2
486 | 2
243 | 3
81 | 3
27 | 3
9 | 3
3 | 3
1

Então depois de tudo isso, chegamos à:
${2}^{5} . {3}^{5}$

Lembre-se: Em potenciação, se os expoentes são iguais e as bases diferentes, basta multiplicar as bases e conservar os expoentes, logo:

${2}^{5} . {3}^{5}\,=\, {6}^{5}$

Então ficamos com:

${6}^{x} \,=\, {6}^{5}$

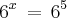
Cancele as bases iguais, e fique com: x = 5

Logo, o log de 7776 na base 6 é 5:

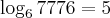
$\log_{6}7776 = 5$

E nesse caso aqui?

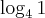
$\log_{4}1$

Log de 1 na base 4! E agora? Que logaritmo que elevado na base 4 pode dar 1?
Hum... Aqui caímos numa convenção: Não importando a base, qualquer número elevado à zero, resultará 1.
Ué, então nesse caso o logaritmo de 1 na base 4 é o zero:

${4}^{0} = 1$

E aqui?

$\log_{8}1$

Mesma coisa... 1 no logaritmando, então o log é zero:
${8}^{0} = 1$

$\log_{8}1 = 0$

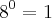
E agora aqui:

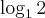
$\log_{1}2$

Opa! Daí temos o número 1 na base, e segundo a condição de existência dos logaritmos, a base deve ser maior que zero e diferente de 1, logo, esse logaritmo não existe!

Agora iremos resolver logs envolvendo frações:

Nesse caso:

$\log_{2}\frac{1}{8}$

O que fazer?

Aqui nós devemos lembrar de algumas propriedades da potenciação, vamos lá?

Primeiramente vamos transformar esse log numa equação exponencial:

${2}^{x} = \frac{1}{8}$

Agora sim podemos visualizar melhor como iremos resolver esse log!

Aqui podemos nos perguntar: Que número que elevado à base 2 dará 1 oitavo?

Vamos começar fatorando o número 8, para ficar igualado à 2:

8 | 2

4 | 2

2 | 2

2³

Então:

${2}^{x} = \frac{1}{{2}^{3}}$

Agora temos uma potência no denominador de uma fração, onde o numerador é 1! Se você se recordar das propriedades da potenciação, sabemos que uma delas nos diz que podemos eliminar esse numerador 1 passando a potência pra cima da fração, apenas trocando o sinal de seu expoente:

$\frac{1}{{2}^{3}} = {2}^{-3}$

Nossa equação fica assim:

${2}^{x} = {2}^{-3}$

Cancelando as bases iguais, teremos: x= -3

Logo, o log de 1 sobre oito na base 2 é três negativo:

$\log_{2}\frac{1}{8} = -3$

Vamos resolver esse log agora:

$\log_{9}\frac{1}{27}$

Primeiramente podemos tentar igualar ambas as bases, vamos começar pelo 9:

9| 3

3| 3

3²

E agora o 27, que é denominador de 1 e pode ser fatorado:

27| 3

9 | 3

3 | 3

3³

Então teremos:

$({3}^{2}){}^{x}=\frac{1}{{3}^{3}}$

À esquerda da equação, temos uma potência de potência, então podemos aplicar uma das propriedades da potenciação, que diz que numa potência de potência, podemos multiplicar os expoentes, logo ficamos com:

$({3}^{2}){}^{x}= {3}^{2x}$

Já no lado direito da equação, temos uma divisão de potências: Novamente podemos aplicar uma das propriedades da potenciação para resolvermos esse caso! Lembre-se: Se temos o 1 no numerador de uma fração, e uma potência no denominador, basta subirmos essa potência pro numerador, eliminar o 1, e trocar o sinal do expoente, então:

$\frac{1}{{3}^{3}} = {3}^{-3}$

Nossa equação ficou assim:

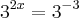
${3}^{2x} = {3}^{-3}$

Vamos cancelar as bases que são iguais, e teremos agora uma equação de primeiro grau:

2x = -3

Resolvendo essa equação simples, temos:

$x = -\frac{3}{2}$

Então o log de um vinte e sete avos, na base 9 é igual à 3 meio negativo:

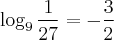
$\log_{9}\frac{1}{27} = -\frac{3}{2}$

E esse aqui:

$\log_{\frac{1}{3}} 81$

Nesse caso temos uma fração na base! Mas a gente pode resolver esse também: Que número que é elevado à um sobre três que dará 81?

${\frac{1}{3}}^{x} = 81$

Podemos decompor esse 81 até três:

81 | 3

27 | 3

9 | 3

3 | 3

Logo:

${\frac{1}{3}}^{x} = {3}^{4}$

Vamos aplicar a propriedade da potência de divisão, novamente:

${\frac{1}{3}}^{x} = {3}^{-1x} = {3}^{-x}$

Então:

${3}^{-x} = {3}^{4}$

Cancele as bases iguais e fique com: -x = 4

Como não queremos nossa incógnita negativa, multiplique os dois lados da equação por -1 e troque os sinais de todos os membros da equação:

(-1)-x = 4 (-1) = x= -4

Então o log de 81 na base de um terço, é igual à quatro negativo:

$\log_{\frac{1}{3}} 81 = -4$

Bem, veja que resolver logs com frações não é tão difícil assim, basta aplicarmos os conceitos já vistos em potenciação, e se necessário, fatorar os números possíveis para igualarmos as bases.

Mas e no caso de logaritmos envolvendo raízes?

$\log_{2} \sqrt[]{8}$

O que fazer neste caso?

Aqui também não tem muito segredo: Basta transformarmos aquela raiz num número com expoente fracionário! Não lembra? Na aula sobre raízes você pode aprender como fazer este tipo de conversão, vamos ver aqui na prática?

Então temos:

${2}^{x} = \sqrt[]{8}$

Antes de você pensar em fazer algo com esta raiz, vamos fatorar o número 8 para se tornar um base em comum com o dois, certo?

8 | 2

4 | 2

2 | 2

Então:

${2}^{x} = \sqrt[]{{2}^{3}}$

Agora sim podemos nos preocupar com a raiz! Lembre-se da aula sobre raízes, o modo como podemos transformar uma raiz num número de expoente fracionário: Basta retirar o radicando de dentro da raiz, feito isso teremos uma fração onde o expoente do radicando será o numerador e o índice da raiz, o denominador, então:

$\sqrt[]{{2}^{3}} = {2}^{\frac{3}{2}}$

Viu? Agora temos nossa equação exponencial da seguinte forma:

${2}^{x} = {2}^{\frac{3}{2}}$

Cancelando as bases iguais, ficamos com: x = 3/2

E está terminado! O log de raiz de 8 na base 2, é três meio:

$\log_{2} \sqrt[]{8}\,=\,\frac{3}{2}$

Continuando... Vamos fazer mais alguns exercícios envolvendo raízes para fixar a ideia?

Tente fazer agora esse log: (Resolução logo abaixo)

$log_{2} \sqrt[6]{16}$

Bem, vamos lá...

A equação então é:

${2}^{x} = \sqrt[6]{16}$

Primeira coisa a se pensar antes de tentar fazer algo com a raiz, é tentar igualar as bases fatorando um dos números, então:

16 | 2
8 | 2
4 | 2
2 | 2
1

Agora temos a seguinte equação:

${2}^{x} = \sqrt[6]{{2}^{4}}$

Vamos radiciar essa raiz para podermos ter bases iguais:

Radiciando, podemos eliminar a raiz fazendo com que o radicando seja um número cujo expoente é fracionário.
Nessa fração, o expoente do radicando será o numerador, e o índice da raiz será o denominador:

$\sqrt[6]{{2}^{4}} = {2}^{\frac{4}{6}}$

Agora note que podemos simplificar essa fração por dois:

${2}^{\frac{4}{6}} = {2}^{\frac{2}{3}}$

Feito isso, nossa equação fica assim:

${2}^{x} = {2}^{\frac{2}{3}}$

Agora podemos cancelar as bases iguais e ficar com x = 2/3
Logo, o log da raiz sexta de 16 na base 2 é dois terços.

$log_{2} \sqrt[6]{16}= \frac{2}{3}$

Vamos resolver mais uma?

$log_{5} \sqrt[4]{625}$

Então... nesta altura do campeonato, você já deve saber como proceder, certo?

Vamos fatorar o 625:

625 | 5
125 | 5
25 | 5
5 | 5
1

Teremos então:

${5}^{x} = \sqrt[4]{{5}^{4}}$

Note que podemos cancelar o expoente do radicando, com o índice da raiz por serem iguais, então:

${5}^{x} = 5$

Lembre-se que quando não temos escrito uma potência num número, isso quer dizer que o número está elevado à um, logo:

${5}^{x} = {5}^{1}$

Então cancelando as bases, x =1
Conclusão: O logaritmo da raiz quarta de 625 na base 5 é igual à 1.

$log_{5} \sqrt[4]{625} = 1$

Logaritmos Decimais:
Você acabou de conhecer os logaritmos com bases diferentes de 10, mas há também os logaritmos decimais que podem ser escritos todos com base 10, e Napier afirmou que poderia representar qualquer número inteiro através dos logaritmos decimais! Como?
Veja este exemplo:

$log_{10}100$

Então podemos ler este log como o logaritmo de 100 na base 10. Mas em logaritmos decimais não precisamos necessariamente escrever a base 10, podemos simplesmente dizer ''log de 100'' que já entenderíamos que se trata de um logaritmo decimal, ou um logaritmo em base 10.
Assim como nos índices de raízes quadradas que não precisa ser escrito o número dois, nos logs decimais não se é necessário escrever a base 10, então:

log100

Trata-se de um logaritmo decimal.

Podemos dizer também que:

log10 = 1

Ou seja, o logaritmo de 10 é igual à 1.
Isso porque na verdade temos um logaritmo de base decimal, onde podemos pensar da seguinte forma: ''Que número que elevado à base 10 possa ser 10?'' 1, certo? Veja:

10¹ = 10

E no caso de:

log100

Pense: "Que número que elevado à base 10 pode dar 100?''
O 2, não? Pois: 10² = 10.10 = 100
Então:

log 100 = 2

Ou seja, o logaritmo de 100 é dois.
Um massete legal para descobrirmos os logs de números de potências do 10 é contado a quantidade de zeros que esse número possui, por exemplo:

log 1000 = 3

Log de 1000 é três por ter 3 zeros! Vejamos outros exemplos:

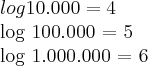
$log 10.000 = 4\par log 100.000 = 5\par log 1.000.000 = 6\par$

*Detalhes: O logaritmo de 1 = 0
E o número 0 não possui logaritmo!

Mas e no caso de números negativos? Como por exemplo: log 0,1?
Bem, note que log de 0,1 é o mesmo que:

$log \frac{1}{10}$

Veja que pela propriedade das frações, podemos escrever esse log da seguinte forma:

$\rightarrow log0,1$

Então o logaritmo de 0,1 é -1.
Perceba que em 0,1 temos um zero, e o resultado foi negativo, logo, podemos concluir que: Todo logaritmo menor que 1 resultará num número negativo, e no caso dos logs com potência 10, basta contarmos a quantidade de zeros do número:

log 0,01 = -2 Pois possui 2 zeros e é menor que 1;
log 0,001 = -3
log 0,0001 = -4

E assim por diante...

Ok, calcular logaritmos decimais referentes à potência 10 é fácil, basta contar sua quantidade de zeros, e se for um número menor que 1 basta saber que o log desse número será negativo, mas como podemos calcular, por exemplo, o logaritmo de 3?

log 3 = ?

Mas como calcular um logaritmo decimal?
Bem, não é uma tarefa muito difícil calcular logaritmos decimais, basta ter conhecimento sobre as quatro propriedades operatórias dos logaritmos (que serão explicadas na próxima aula) ou saber consultar a tábua logarítmica!
Sim, a tábua logarítmica! Lembra-se no início da aula onde foi explicado que esta tábua de logaritmos poderia vir a ser muito útil para épocas remotas onde não existiam calculadoras? Então, aqui você vai aprender a consultar essa tábua (que na verdade é uma tabela) e vai saber como aplicá-la nos logaritmos decimais.

Tábua de Logaritmos:
Essa tábua logarítmica possui duas colunas seguindo uma propriedade: Multiplicar dois números da coluna da esquerda, é a mesma coisa que somar esses números correspondentes na coluna da direita.
E isso facilitaria muitos a resolução de cálculos muito complexos, pois uma soma é muito mais fácil de ser resolvida do que uma multiplicação, por exemplo. Veja um exemplo:
Aqui temos uma parte da tábua de logaritmos:

Suponhamos que gostaríamos de saber o resultado da multiplicação: 2.5
Claro, todos sabemos que é 10 por ser uma conta mais simples, mas veja como os logaritmos podem nos auxiliar nesse tipo de tarefa:
Ao invés de multiplicarmos 2 por 5, poderíamos somar os logaritmos desses números, ou seja:
0,30103 + 0,69897 = 1
Note que a soma desses logaritmos nos resulta em 1, e 1 é exatamente o logaritmo de 10, o produto da multiplicação de 2.5! Incrível, não?

Vejamos outro exemplo:

Queremos saber então quanto é 16.6! Ao invés de realizar essa multiplicação, poderíamos facilmente somar os logaritmos dos números correspondentes. Clique aqui para acessar a tabela de logaritmos de 1 à 99.
Procure pelos logaritmos de 16 e 6 e depois some ambos:
1,20412 + 0,778151 = 1,982271
Agora procure pelo número que corresponde à esse logaritmo (1,982271), e encontre 96!
Perceba que 16*6 = 96, exatamente o número correspondente à soma dos logs de 16 e 6!

Pois bem, a tábua logarítmica é muito eficiente mesmo, mas o que fazer quando estamos sem ela?
Para isso, precisamos saber calcular os logaritmos decimais e conhecer suas quatro propriedades fundamentais operatórias!
Então para conhecê-las, leia a próxima aula sobre o assunto, clicando aqui!

2 comentários:

Anônimo25 de setembro de 2017 às 08:05
Amei sua explicação. Não consegui compreender as aulas do professor, mas aqui aprendi. Obrigada
ResponderExcluir
Respostas
MayLeone15 de outubro de 2018 às 05:26
Muito obrigada, fico muito feliz por ter conseguido te ajudar.
Espero que tenha bons estudos e tire notas altas na prova. <3
ResponderExcluir
Respostas

Adicionar comentário

Aulas da May

sexta-feira, 30 de maio de 2014

Logaritimos: Conceitos Iniciais

2 comentários:

Entre em contato: