Os pontos numa circunferência:
Se você leu a aula sobre circunferências, você deve se lembrar que: A circunferência é um local geométrico, onde todos os pontos que a formam tem a mesma distância de um ponto central, assim:
Você deve se lembrar também que: A medida entre um ponto qualquer da circunferência até seu centro tem o nome de raio.
Você aprendeu a calcular o raio da circunferência caso você saiba a área ou o comprimento da mesma, mas e se não tivermos essas informações? Como proceder? Como encontrar a medida do raio?
Para isso, alguns matemáticos deduziram uma fórmula para criarmos a equação da circunferência, onde com ela poderíamos calcular essas distâncias, veja abaixo:
Equação Reduzida:
A equação reduzida da circunferência é a equação ''abreviada'' da equação geral da mesma (em breve será mostrada) e que nós utilizamos para calcular a distância entre o Centro da circunferência (ou que nós podemos chamar de ponto C) e um ponto qualquer na mesma.
Se uma circunferência é um local geométrico onde todos seus pontos são equidistantes (ou seja, tem a mesma distância) do seu centro, como podemos calcular a distância entre o ponto C (centro) e outro ponto qualquer da circunferência?
Veja uma representação dessa situação na imagem abaixo...
Como podemos saber a distância que tem o ponto P na circunferência, até o centro da mesma?
E as distâncias entre o centro da circunferência e os pontos Q, R, S, T, U e etc..?
Para isso, utilizamos as equações da circunferência, que nos possibilita descobrir distâncias entre pontos da circunferência e seu centro, e descobrir também se determinado ponto pertence à essa circunferência.
Deduzindo a fórmula da equação reduzida:
Nessa parte da aula, eu irei lhe explicar como a fórmula da equação reduzida da circunferência foi deduzida.
Para encontrarmos a equação da circunferência, primeiro devemos definir a fórmula da distância entre dois pontos, sendo que esses pontos devem ter coordenadas x e y.
Para encontrarmos as coordenadas para os pontos de uma circunferência, vamos utilizar o plano cartesiano para isso:
Aqui está, um plano cartesiano com a abcissa x, ordenada y e a nossa circunferência.
Iremos então determinar um ponto qualquer para a circunferência, seu centro, por exemplo. Chame o centro de ponto C, e vamos estipular as coordenadas desse ponto, por exemplo, a e b:
Então para o centro dessa circunferência teremos as coordenadas C=(a,b)
Agora que você sabe como utilizar o plano cartesiano para estipular as coordenadas para um ponto para a circunferência, vamos definir a fórmula da distância entre dois pontos.
Então vamos estipular dois pontos qualquer para a circunferência: Vamos chamar esses pontos de A e B:
E vamos dar coordenadas à esses dois pontos. Para A = (x¹, y¹) e para B = (x², y²)
Vamos traçar os segmentos para esses pontos:
Definindo uma coordenada qualquer para o ponto C na a circunferência, teremos:
Se você criar os segmentos à partir desses três pontos, iremos obter:
Um triângulo retângulo de vértices ABC!
Tomamos do princípio que entre o ponto A e o ponto C teremos: AC = x²-x¹ (A distância entre as coordenadas x dos pontos A e B)
A coordenada ''x²'' vem primeiro na subtração, porque é maior que ''x¹'', visto que ela se encontra mais à direita da reta x no plano cartesiano.
E entre o ponto B e o ponto C, teremos: BC = y²-y¹ (distância das coordenadas y dos pontos A e B)
Logo:
Então temos os lados AC E BC como os catetos do triângulo retângulo.
Referente ao ângulo reto de 90 graus, o lado AB é a hipotenusa, e também é a distância entre os pontos A e B.
Então para encontrarmos o lado AB do triângulo, podemos aplicar o Teorema de Pitágoras referente aos triângulos retângulos:
h² = l² + l²
Onde ''h'' é a hipotenusa e ''l'' são os lados.
Teremos:
AB² = AC² + BC²
Se AC = (x²-x¹) e BC = (y² -y¹) Teremos na fórmula:
AB² = (x²-x¹)² + (y²-y¹)²
Passando o expoente 2 de AB para o outro lado do sinal, iremos obter:
![AB\,=\,\sqrt[]{(x²-x¹)² + (y²-y¹)²}](http://www.ajudamatematica.com/latexrender/pictures/4b3fd37b6b056a4edbcdb61c3aceae69.png)
E essa é a fórmula da distância entre dois pontos.
Agora que definimos a fórmula da distância entre dois pontos, vamos aplicar essa ideia, para determinarmos a fórmula da equação da circunferência.
Vamos imaginar que temos uma circunferência cujo centro = C (x,y)
Lembre-se sempre: O raio da circunferência, é a distância entre seu centro até um ponto qualquer na mesma, como visto nas aulas sobre circunferências!
Se o raio da circunferência é a distância entre o centro até um ponto qualquer da mesma, vamos chamar esse ponto qualquer de ponto P, e definir suas coordenadas (a,b)
Então aplicando esses conceitos na fórmula da distância entre dois pontos teremos: A coordenada ''x'' na abcissa do centro, e na abcissa do ponto P teremos a coordenada ''a''. Para a ordenada do centro teremos ''y'' e para ordenada do ponto P, teremos ''b'', onde a distância entre esses pontos será o raio da circunferência:
Ponto C = (x,y)
Ponto P = (a,b)
![\sqrt[]{(a-x)² + (b-y)²} = R](http://www.ajudamatematica.com/latexrender/pictures/f40518d1edcabf9e39a60f2288f673d7.png)
Para eliminarmos essa raiz da fórmula, podemos elevar os dois lados da equação ao quadrado:
![(\sqrt[]{(a-x)² + (b-y)²})² = R²](http://www.ajudamatematica.com/latexrender/pictures/f33ddfac89af77f11fc0ad6ffe09be7d.png)
Agora com esse expoente dois na raiz, podemos radiciar a mesma e eliminar essa raiz quadrada:

E esta é a fórmula reduzida da equação da circunferência, onde ''a'' e ''b'' são as variáveis, ou seja, as coordenadas de um ponto qualquer na circunferência, e ''x'' e ''y'' são constantes, ou seja, as coordenadas do centro da circunferência.
Verificando os pontos numa circunferência:
Então agora chega de teorias, vamos ver na prática como utilizar a fórmula da equação reduzida da circunferência:
Como já mencionando, a equação reduzida da circunferência, é uma forma prática de encontrarmos a medida do raio da mesma, e de verificar se um ponto passa pela nossa circunferência ou não, tudo isso com o auxílio da fórmula mostrada acima.
Vamos imaginar que temos uma circunferência, cujo centro têm as coordenadas (x,y) = (2,1) Ou seja, coordenada x = 2 e coordenada y = 1.
Substituindo as coordenadas do centro (x,y) na fórmula da equação reduzida, nós teremos:

E vamos supor que o raio dessa circunferência seja igual ao quadrado de 5:

E aqui está a equação dessa circunferência cujo centro (C) tem coordenadas (3,1) e o raio é igual à 5 ao quadrado.
Agora podemos substituir em ''a'' e ''b'' na fórmula, as coordenadas de um ponto qualquer (podemos chamar de ponto P mesmo) que queremos verificar se ele pertence ou não à essa circunferência.
Como saber se o ponto ''P'' pertence à circunferência? Simples, se as coordenadas dele (que serão inseridas na fórmula), igualarem a equação, ou seja, dizer que a distância entre as coordenadas do centro e as coordenadas deste ponto, forem iguais ao quadrado do raio, esse ponto pertencerá à circunferência, do contrário, esse ponto não pertence à circunferência
 .
.Vamos ver como que fica? Vamos verificar se o Ponto P(6,-2) pertence à essa circunferência.
Lembre-se: ''6'' é a coordenada x (ou ''a'' na fórmula'') e ''-2'' a coordenada y (ou ''b'' na fórmula)
A equação fica assim:
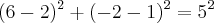
Fazendo as contas:


Confere! Pois 16 + 9 dará 25, logo a equação é verdadeira e o ponto P(6,-2) pertence à circunferência

Viu? Não é tão difícil, basta lembrar que na fórmula, ''x'' e ''y'' são referentes às coordenadas do centro, e ''a'' e ''b'' são referentes às coordenadas do ponto que você deseja verificar.
Quer ver mais um exemplo?
Determine a equação das circunferências à seguir, sabendo o centro e o raio:
A) C(1,-4) R = 4
B) C(2,6) R = 2
C) C(-5,-3)R = √49
D) C(12,9) R = x + 4x + 2 = 3x + 18
Resoluções:
A) Se o centro tem coordenadas (1,-4) e raio igual à 4, logo teremos na fórmula:
![(a-1)² + (b-[-4])²= 4²\, ou\, (a-1)² + (b +4 )²= 16](http://www.ajudamatematica.com/latexrender/pictures/95dd4af476634eb7dcad0569e679a068.png)
B) Centro: (2,6) e Raio = 2, então:

C) Centro(-5,-3) Raio = raiz de 49 teremos
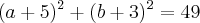
D) Vamos resolver a equação primeiro para descobrirmos o raio:
x + 4x + 2 = 3x + 18
5x - 3x = 18 - 2
2x = 16
x= 16/2
x= 8
Então temos C(12,9) e Raio = 8

Note que as coordenadas (tanto do centro, quanto de qualquer ponto) sempre trocam de sinal quando são inseridas na fórmula da equação reduzida.
Se por exemplo, temos as coordenadas de C(-22,-10) na fórmula, ''-22'' e ''-10'' ficarão positivos:

E acontece o mesmo com coordenadas positivas. Se temos por exemplo: C(7,1) na fórmula teremos:
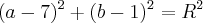
Sabendo disso, determine o centro das equações das circunferências abaixo:




Resoluções:
A) Centro(18,-3)
B) Centro(1,4)
C) Centro(-14,6)
D) Centro(-8,-5)
Viu? Se uma coordenada era positiva, na fórmula vira negativa, e se uma coordenada era negativa, na fórmula fica positiva.
Isso acontece por conta da regra dos sinais, onde:
+ + = +
+ - = -
- + = -
- - = +
Veja melhor novamente no primeiro exemplo desses exercícios:
A) Se o centro tem coordenadas (1,-4) e raio igual à 4, logo teremos na fórmula:
![(a-1)² + (b-[-4])²= 4²\, ou\, (a-1)² + (b +4 )²= 16](http://www.ajudamatematica.com/latexrender/pictures/95dd4af476634eb7dcad0569e679a068.png)
Veja nessa parte da fórmula: (b-[-4])² onde temos sinal negativo com sinal negativo, logo, esse sinal ficará positivo: (b+4)²
Encontrar as coordenadas do centro numa equação reduzida você já sabe, mas e o raio?
Determine a equação da circunferência, onde o centro tem coordenadas (3,1) e que passa pelo ponto D(6,3).
A primeira coisa que devemos fazer é determinarmos quem é ''x'' e ''y'' na fórmula, e também quem é ''a'' e ''b''.
Coordenadas x e y se referem ao centro, logo x=3 y= 1
Já para ''a'' e ''b'' temos a=6 e b=3
Então nossa equação fica assim:

Para descobrimos o raio da circunferência (6-3)² + (3-1)² basta resolver a equação:




![R = \sqrt[]{13}](http://www.ajudamatematica.com/latexrender/pictures/d8369f311b476c4a38ec6f6d379edb72.png)

Então o raio dessa circunferência é de aproximadamente 3,6 ou raiz de 13.
Ou seja, a distância entre o centro dessa circunferência até o ponto P é de aproximadamente 3,6.
No gráfico fica mais ou menos assim:
Ponto médio e Mediatriz:
Vamos imaginar uma reta de segmentos AB:
Tendo esse segmento, o ponto médio (m) é o ponto onde corta-se essa reta ao meio:
Note que o ponto médio está bem ao meio de A e B, formando duas partes: MA e MB.
Bom, este é o ponto médio, certo, mas e a Mediatriz?
Já a Mediatriz, é uma reta perpendicular, ou seja, que forma um ângulo reto de 90 graus, que passa pelo ponto médio:
Agora imagine essa situação na circunferência:
Dada uma circunferência, e pontos A e B:
Traçando uma reta para os pontos A e B, temos então a corda AB:
À partir do ponto médio, podemos encontrar a mediatriz da corda AB:
Note que essa mediatriz passa pelo centro da circunferência! O que? Não acredita?
Então vamos lá de novo...
Dada uma circunferência com os pontos L e N e o ponto P para o centro, teremos:
Trace a reta para os pontos L e N e à partir da corda LN, determine seu ponto médio:
Agora trace a mediatriz de LN à partir do ponto médio:
Note que a Mediatriz de LN passa pelo centro (P) da circunferência, e não importa como os pontos L e N estejam distribuídos na circunferência, a mediatriz SEMPRE passará pelo centro, isto se os pontos L e N pertencerem à circunferência.
Logo, temos a propriedade:
"Se dois pontos A e B pertencem a uma circunferência, a mediatriz de AB passa pelo centro."
*Nunca se esqueça que: A distância entre um ponto qualquer da circunferência e seu centro é o raio da mesma, logo, o raio dessa circunferência pode ser representado pelos segmentos PN e PL:
Mas como calcular o ponto médio de um segmento?
Você já viu que o ponto médio (m) de um segmento é o local geométrico que corta esse segmento ao meio, ou seja, que está no centro desse segmento, e sabe também que para encontrarmos a mediatriz de um segmento, precisamos antes determinar o ponto M para o mesmo, então você se pergunta... Como que se calcula o ponto médio de uma circunferência?
Então vamos lá, vou explicar aqui como podemos calcular o ponto médio de um segmento:
Os pontos A e B numa circunferência, possuem coordenadas: A(x1, x2) e B(x2,y2):
Para encontrarmos o ponto médio entre esses pontos, vamos relacionar suas distâncias, primeiramente:
Relacionando a distância x¹ (Ponto A) e x² (Ponto B), podemos somá-las e depois dividi-las por dois, para encontrarmos justamente a metade de suas distâncias, ou seja, o meio entre elas:

Ou seja, o resultado dessa conta, será exatamente a medida do meio das distâncias x¹ e x² dos pontos A e B, no plano cartesiano, para a abcissa.
Tomando ainda o mesmo raciocínio, podemos fazer o mesmo com as distâncias y¹ e y²:

Aqui iremos obter o resultado da medida do meio das distâncias y¹ e y² dos pontos A e B, pela ordenada no plano cartesiano.
Perceba que com isso podemos encontrar as coordenadas do ponto médio do segmento AB, no plano cartesiano!
Logo, temos a seguinte fórmula para calcularmos o ponto médio de qualquer segmento:

Vejamos um exemplo:
Tendo dois pontos A e B numa circunferência, onde A (4; 6) e B(2; 4), determine o ponto médio entre a corda AB.
Vamos desenhar primeiramente a circunferência e o plano cartesiano, contendo essas medidas:
Agora encontre as coordenadas para A e B:
Após encontrar os pontos A e B, crie a corda AB:
Finalmente iremos utilizar a fórmula para encontrarmos as coordenadas do ponto médio(m) nesse segmento, utilizando a fórmula:

Onde x¹ e y¹ serão as coordenadas do ponto A e x² e y² serão as coordenadas do ponto B, teremos:

Então:

6 dividido por 2 dá 3, e 10 dividido por 2 é 5, logo, as coordenadas do ponto M desse segmento são (3; 5)
Jogando no gráfico iremos ter:
O ponto médio desse segmento!
''Mas pra quê eu uso o ponto médio?''
R: Não lembra? Para determinarmos a mediatriz do segmento!
"Tá, e pra quê eu uso a mediatriz?''
R: Ué, com a mediatriz nós podemos encontrar o centro da circunferência! Quer ver?
Desenhe a sua circunferência:
Agora determine três pontos qualquer nessa circunferência (onde você quiser, contanto que os três pontos não fiquem alinhados):
Depois, crie as cordas AB e BC:
Feito isso, encontre o ponto médio em cada uma das cordas:
Em seguida, trace a mediatriz da corda AB à partir do seu ponto médio:
Por fim, trace a mediatriz da corda BC:
A intersecção das duas mediatrizes, será o centro da circunferência!
Distância entre o centro e uma reta tangente à circunferência:
Nesta parte da aula, você aprenderá a calcular a distância entre o centro da circunferência, até uma reta tangente à mesma.
Mas como assim ''reta tangente à circunferência?''
Pois bem, o ponto de tangência indica que determinado elemento (no caso uma reta), está encostando em um dos pontos da nossa circunferência, por exemplo, assim:
Note que a reta A tangência, ou melhor, ''toca'' a circunferência. O segmento em lilás da imagem, é justamente a distância entre a Reta A que é tangente à circunferência, até o centro da mesma, e isso é exatamente o que iremos aprender a calcular aqui.
Pois bem, veja que podemos calcular essa distância, que seria na verdade o raio desta circunferência, certo?
Vamos ver isso na prática...
Determine a equação da circunferência, com centro no ponto (3,2) e com uma reta tangente à circunferência, sendo que a reta é: 2x + y + 7 = 0
Note que nossa equação poderia ficar da seguinte forma:
(x-3)² + (y-2)² = r²
Mas perceba que para a equação ficar completa, necessita-se do raio da mesma, e para encontrar o raio, basta calcularmos a distância entre a reta que tangência a circunferência até o centro da mesma, vamos lá?
Vamos por partes:
Equação da circunferência:
(a-x)² + (b-y)² = r²
Equação da reta:
Ax + By + C = 0
As coordenadas são: Para o centro da circunferência: (3,2)
Para a reta: A = 2 B = 1 C = 7
Agora vamos utilizar uma fórmula específica para esses casos, da distância entre dois pontos, entre um ponto da circunferência e uma reta qualquer:
![\frac{(a.A + b.B + C)}{\sqrt[]{A² + B²}}](http://www.ajudamatematica.com/latexrender/pictures/2660ac7046b0a613f9affd83a844951a.png)
Veja que apesar de parecer, a fórmula não é tão complexa assim, basta substituir os valores na mesma.
Para ''a'', temos a coordenada x do centro da circunferência, que é 3; para ''b'' temos a coordenada y do centro da mesma, que é 2; já para as coordenadas da reta, como já mostrado anteriormente, temos: A = 2, B = 1 e C = 7.
Vamos então substituir os valores na fórmula:
![\frac{(3.2 + 2.1 + 7)}{\sqrt[]{2² + 1²}}](http://www.ajudamatematica.com/latexrender/pictures/c99f1659dd80d3386d8a2a489bd3fa73.png)
Perceba que agora basta realizarmos as operações! Vamos fazer o que há no numerador primeiro: (3.2) = 6 --> 2.1 = 2 --> logo: 6 + 2 + 7 = 15
![\frac{15}{\sqrt[]{2² + 1²}}](http://www.ajudamatematica.com/latexrender/pictures/465db3798f1bd214c8f107573d6f8efa.png)
Agora podemos fazer o que há no denominador!
Realize as potências: 2² = 4 e 1² = 1 --> 4 + 1 = 5
Ficamos com:
![\frac{15}{\sqrt[]{5}}](http://www.ajudamatematica.com/latexrender/pictures/6a125d581b3b698a52e16d90083b54d1.png)
Agora radicalize essa fração:
![\frac{15}{\sqrt[]{5}} . \frac{\sqrt[]5{}}{\sqrt[]{5}} = \frac{15\,\sqrt[]{5}}{5} = 3\,\sqrt[]{5}](http://www.ajudamatematica.com/latexrender/pictures/fd9084b8128fffe13f6602031667acfa.png)
Por fim, encontre o valor de 3 raiz de 5, multiplicando a raiz de 5 por 3, que é aproximadamente: 6,7.
Portanto, a distância entre essa reta tangente à circunferência, até o centro da mesma, é de aproximadamente 6,7! Ou seja, o raio dessa circunferência!
Logo, nossa equação da circunferência, fica da seguinte forma:
(x-3)² + (y-2)² = 6,7² ou (x-3)² + (y-2)² = 44,89
Outro exemplo?
Determine a equação da circunferência, cujo centro é C(2,1), que é tangente à reta: 3x - 4y + 8 = 0
Sem o raio, nossa equação da circunferência ficaria assim:
(x - 2)² + (y - 1)² = r²
Mas nós precisamos do raio desta circunferência para completar a equação.
Podemos tomar como referência, essa reta que tangência a circunferência, pois a distância entre ela e o centro da circunferência, seria exatamente o raio que procuramos.
Sabendo desta relação, basta aplicarmos a fórmula mostrada mais acima, para encontrarmos essa distância:
![\frac{(a.A + b.B + C)}{\sqrt[]{A² + B²}}](http://www.ajudamatematica.com/latexrender/pictures/2660ac7046b0a613f9affd83a844951a.png)
Vamos ver quem é quem:
Centro da circunferência: (2,1), ''a'' e ''b'' na fórmula, respectivamente;
A => 3
B => -4
C => 8
Então:
![\frac{(2.3 + 1.-4 + 8)}{\sqrt[]{3² + 4²}}](http://www.ajudamatematica.com/latexrender/pictures/851ee9ed398206475a9ba81753facf90.png)
Fazendo primeiramente o numerador da fração, temos:
2.3 --> 6 + 1.(-4) --> -4 então: 6 + 8 - 4= 10
![\frac{10}{\sqrt[]{3² + 4²}}](http://www.ajudamatematica.com/latexrender/pictures/3edef453eab2c5ad594c3f3a0350fb1f.png)
Agora resolvendo o denominador: 3² = 9 e 4² = 16 --> 9+16 = 25
Lembrando que temos ainda uma raiz e 25 está dentro desta raiz, então ficamos com a raiz quadrada de 25 que é igual à 5:

Por fim, divida 10 por 5 e obtenha 2, o raio desta circunferência.
Nossa equação fica da seguinte forma:
(x - 2)² + (y - 1)² = 2² ou (x - 2)² + (y - 1)² = 4
Pois bem, veja que podemos calcular essa distância, que seria na verdade o raio desta circunferência, certo?
Vamos ver isso na prática...
Determine a equação da circunferência, com centro no ponto (3,2) e com uma reta tangente à circunferência, sendo que a reta é: 2x + y + 7 = 0
Note que nossa equação poderia ficar da seguinte forma:
(x-3)² + (y-2)² = r²
Mas perceba que para a equação ficar completa, necessita-se do raio da mesma, e para encontrar o raio, basta calcularmos a distância entre a reta que tangência a circunferência até o centro da mesma, vamos lá?
Vamos por partes:
Equação da circunferência:
(a-x)² + (b-y)² = r²
Equação da reta:
Ax + By + C = 0
As coordenadas são: Para o centro da circunferência: (3,2)
Para a reta: A = 2 B = 1 C = 7
Agora vamos utilizar uma fórmula específica para esses casos, da distância entre dois pontos, entre um ponto da circunferência e uma reta qualquer:
![\frac{(a.A + b.B + C)}{\sqrt[]{A² + B²}}](http://www.ajudamatematica.com/latexrender/pictures/2660ac7046b0a613f9affd83a844951a.png)
Veja que apesar de parecer, a fórmula não é tão complexa assim, basta substituir os valores na mesma.
Para ''a'', temos a coordenada x do centro da circunferência, que é 3; para ''b'' temos a coordenada y do centro da mesma, que é 2; já para as coordenadas da reta, como já mostrado anteriormente, temos: A = 2, B = 1 e C = 7.
Vamos então substituir os valores na fórmula:
![\frac{(3.2 + 2.1 + 7)}{\sqrt[]{2² + 1²}}](http://www.ajudamatematica.com/latexrender/pictures/c99f1659dd80d3386d8a2a489bd3fa73.png)
Perceba que agora basta realizarmos as operações! Vamos fazer o que há no numerador primeiro: (3.2) = 6 --> 2.1 = 2 --> logo: 6 + 2 + 7 = 15
![\frac{15}{\sqrt[]{2² + 1²}}](http://www.ajudamatematica.com/latexrender/pictures/465db3798f1bd214c8f107573d6f8efa.png)
Agora podemos fazer o que há no denominador!
Realize as potências: 2² = 4 e 1² = 1 --> 4 + 1 = 5
Ficamos com:
![\frac{15}{\sqrt[]{5}}](http://www.ajudamatematica.com/latexrender/pictures/6a125d581b3b698a52e16d90083b54d1.png)
Agora radicalize essa fração:
![\frac{15}{\sqrt[]{5}} . \frac{\sqrt[]5{}}{\sqrt[]{5}} = \frac{15\,\sqrt[]{5}}{5} = 3\,\sqrt[]{5}](http://www.ajudamatematica.com/latexrender/pictures/fd9084b8128fffe13f6602031667acfa.png)
Por fim, encontre o valor de 3 raiz de 5, multiplicando a raiz de 5 por 3, que é aproximadamente: 6,7.
Portanto, a distância entre essa reta tangente à circunferência, até o centro da mesma, é de aproximadamente 6,7! Ou seja, o raio dessa circunferência!
Logo, nossa equação da circunferência, fica da seguinte forma:
(x-3)² + (y-2)² = 6,7² ou (x-3)² + (y-2)² = 44,89
Outro exemplo?
Determine a equação da circunferência, cujo centro é C(2,1), que é tangente à reta: 3x - 4y + 8 = 0
Sem o raio, nossa equação da circunferência ficaria assim:
(x - 2)² + (y - 1)² = r²
Mas nós precisamos do raio desta circunferência para completar a equação.
Podemos tomar como referência, essa reta que tangência a circunferência, pois a distância entre ela e o centro da circunferência, seria exatamente o raio que procuramos.
Sabendo desta relação, basta aplicarmos a fórmula mostrada mais acima, para encontrarmos essa distância:
![\frac{(a.A + b.B + C)}{\sqrt[]{A² + B²}}](http://www.ajudamatematica.com/latexrender/pictures/2660ac7046b0a613f9affd83a844951a.png)
Vamos ver quem é quem:
Centro da circunferência: (2,1), ''a'' e ''b'' na fórmula, respectivamente;
A => 3
B => -4
C => 8
Então:
![\frac{(2.3 + 1.-4 + 8)}{\sqrt[]{3² + 4²}}](http://www.ajudamatematica.com/latexrender/pictures/851ee9ed398206475a9ba81753facf90.png)
Fazendo primeiramente o numerador da fração, temos:
2.3 --> 6 + 1.(-4) --> -4 então: 6 + 8 - 4= 10
![\frac{10}{\sqrt[]{3² + 4²}}](http://www.ajudamatematica.com/latexrender/pictures/3edef453eab2c5ad594c3f3a0350fb1f.png)
Agora resolvendo o denominador: 3² = 9 e 4² = 16 --> 9+16 = 25
Lembrando que temos ainda uma raiz e 25 está dentro desta raiz, então ficamos com a raiz quadrada de 25 que é igual à 5:

Por fim, divida 10 por 5 e obtenha 2, o raio desta circunferência.
Nossa equação fica da seguinte forma:
(x - 2)² + (y - 1)² = 2² ou (x - 2)² + (y - 1)² = 4
Equação Geral da circunferência:
Pois bem, você conheceu a equação reduzida da circunferência, mas temos também esta equação em sua forma geral, que pode ser muito útil em casos específicos.
Antes de vermos esses casos particulares, vamos deduzir a equação geral?
Se temos uma equação reduzida da seguinte forma:
(x - a)² + (y - b)² = r²
Para determinar a equação geral, devemos desenvolver essa equação, à partir dos produtos notáveis:
Em: (x-a)² podemos dizer o seguinte:
''O quadrado do primeiro, menos duas vezes o produto do primeiro pelo segundo, mais o quadrado do segundo''.
Logo:
x² - 2ax + a²
Então, temos ainda: (y-b)² que seguirá o mesmo raciocínio:
y² - 2by + b²
Somando tudo, teremos:
x² - 2ax + a² + y² - 2by + b² = r²
Passando o ''r²'' para o outro lado do sinal iremos obter:
x² - 2ax + a² + y² - 2by + b² -r² = 0
Agora basta reorganizar tudo, deixando termos semelhantes próximos de si:
x² + y² - 2ax - 2by + a² + b² - r² = 0
E aí está a equação geral da circunferência, vamos vê-la na prática?
Uma circunferência possui o centro em (2, -1) e raio igual à 5, determine sua equação na forma geral.
Primariamente vamos determinar essa equação na forma reduzida:
(x -2)² + (y+1)² = 25
Agora vamos determinar a equação em sua forma geral, desenvolvendo seus termos:
x² - 2.-2x + 2² + y² + 2.y + 1² = 25
Resolvendo a equação:
x² - 4x + 4 + y² + 2y + 1 = 25
Reagrupando:
x² + y² - 4x + 2y (4+1 - 25) = 0
Perceba que os termos independentes (4, 1 e 25) estão entre parênteses, portanto serão resolvidos.
Resolvendo os termos independentes: 4+1-25 = -20, então:
x² + y² - 4x + 2y - 20 = 0
E está aí a equação da circunferência em sua forma geral.
Mas por que utilizá-la?
Se um problema pedisse para que você encontrasse as coordenadas do centro da circunferência e do raio, de acordo com a equação na forma geral, como fazer?
Vamos pegar o exemplo que acabamos de resolver:
x² + y² - 4x + 2y - 20 = 0
Como definir o centro da circunferência e o seu raio?
Para isso, vamos saber quem é quem, analisando:
''EQ'' -> Equação geral da circunferência
''EP'' -> Nossa equação:
EQ: x² + y² - 2ax - 2by + a² + b² - r² = 0
EP: x² + y² - 4x + 2y - 20 = 0
Vamos então perceber, que como ''a'' e ''b'' não aparecem na nossa equação, eles são iguais à um.
Já o ''-4x'' e ''+2y'' podemos dizer que são o produto da multiplicação de ''a'' e ''b'', respectivamente, então:
-4x -> -4ax
+ 2y -> +2by
Seguindo o raciocínio dos produtos notáveis, ''-4ax'' é o produto do primeiro pelo segundo, duas vezes, então esse número é: 2.(-2).a.x, separadamente.
Como ''x'' é igual à um, então temos por enquanto: (-2a), então para a coordenada x (''a'' na equação) do centro da circunferência, temos: 2 (pois fora da equação, muda-se o sinal).
Agora para +2by -> Podemos notar que esse valor é o produto da multiplicação, do primeiro pelo segundo duas vezes, ou seja: 2.b.y, e notando esse resultado, ''b'' vale 1, ou fora da equação: -1, nossa coordenada y do centro (''b'' na equação).
Por fim, encontramos ''a'' e ''b'' na equação: 2 e -1, respectivamente.
Para o raio, basta notarmos essa parte na equação geral da circunferência:
(a² + b² - r² = 0)
Vamos substituir os valores:
-4 - 1² - r² = 0
Lembre-se, na nossa equação da forma geral, temos um termo independente, o ''-20''e devemos introduzi-lo à este cálculo:
-4 - 1² - 20 + r² = 0
- 5 - 20 + r² = 0
- 25 + r² = 0
Isolando o raio do outro lado do sinal:
r² = 25
E passando o expoente ''2'' do mesmo também para o outro lado do sinal, teremos: √25 = 5, ou seja o raio da circunferência.
Logo, o centro da circunferência é: (2, -1) e o raio da mesma é igual à 5.
Perceba que é exatamente o resultado do exemplo acima, e nós descobrimos isso invertendo os termos apresentados de uma equação geral da circunferência.






































Muito Obrigada ! Tirou todas as minhas duvidas :)
ResponderExcluir