Triângulo Obtusângulo e Acutângulo:
Você aprendeu na aula sobre trigonometria dos triângulos retângulos, a aplicação de diversas relações trigonométricas num triângulo retângulo, que tem como principal característica o ângulo reto de 90 graus.
Se um triângulo qualquer sempre irá possuir 3 ângulos e a soma desses três ângulos deve ser sempre 180 graus, o que resta para um triângulo retângulo são apenas mais dois ângulos agudos (que são menores que 90 graus), pois, se um dos ângulos forem maiores que 90 graus não teríamos mais um triângulo retângulo!
Veja: No triângulo retângulo temos que: 90 graus já é nosso ângulo reto, para somarmos 180 graus nos três ângulos juntos, os outros dois ângulos devem ser necessariamente menores que 90 graus.
Pense bem... Num triângulo com ângulo de 100 graus e mais outros dois ângulos, um com 60 graus e o outro com 20 graus. Quanto daria isso? 100° + 60° + 20° = 180°, certo! Mas num triângulo retângulo já temos sempre um ângulo reto de 90 graus, e nesse caso podemos observar que não temos mais um triângulo retângulo, e sim um triângulo com dois ângulos agudos, ou seja, menores que 90 graus (20 graus e 60 graus) e um ângulo maior que 90 graus! O ângulo de 100 graus.
Os ângulos maiores que 90 graus possuem o nome de ângulos obtusos.
Logo, um triângulo que possui dois ângulos agudos e um ângulo obtuso tem o nome de triângulo obtusângulo.
Geralmente esses triângulos tem esse formato:

Mas e no caso de encontrarmos um triângulo cujos ângulos são todos menores que 90 graus, ou seja, um triângulo que possui todos os ângulos agudos? Como por exemplo um triângulo que tem seus ângulos medindo: 80°, 60° e 40°. Note que todos esses ângulos são agudos e que a soma dos três dará 180 graus -> 60°+40°+80° = 180°
Mas qual o nome para esses tipos de triângulos?
O triângulo que possui todos os seus ângulos agudos recebe o nome de triângulo acutângulo, veja:
Certo, você já percebeu que em ambos os casos nenhum dos dois triângulos acima (obtusângulo e acutângulo) são triângulos retângulos por não possuírem o ângulo reto de 90 graus, logo, nossas aplicações e relações trigonométricas já vistas anteriormente, não se aplicariam para esses casos. E agora?
Agora temos uma solução para o caso desses triângulos especiais, que irá servir para calcular as medidas de qualquer triângulo independente de seus ângulos, veja:
A lei dos Cossenos:
Você já se familiarizou com o cosseno e suas relações com os arcos notáveis na aula de trigonometria do triângulo retângulo, certo? Pois bem, nesta nova aplicação para triângulos não retângulos, iremos utilizá-lo, só que dessa vez de uma forma diferente.
Você saberia me dizer o que as letras A,B e C na figura abaixo nos representa neste triângulo?
Aqui as letras A,B e C nos informa os três ângulos deste triângulo.
Relacionando esses três ângulos com os nossos lados, podemos sempre alinhar o lado ''a'' oposto ao ângulo A, como também o lado ''b'' oposto ao ângulo B e o lado ''c'' oposto ao ângulo C, assim:

Note que as pequenas letras em vermelho, são similares às letras que nos informam os ângulos deste triângulo, e que estão sempre opostas à seus ângulo referentes.
a está oposto ao ângulo A, assim como b está oposto ao ângulo B e c está oposto ao ângulo C.
Com estas relações entre lados e ângulos de triângulos, podemos conhecer a fórmula da Lei do Cosseno, segue:
Para o ângulo A temos que:
a² = b² + c² - 2.b.c.cos A
Aqui a fórmula nos diz que o quadrado do lado a é igual à soma dos quadrados dos lados b e c menos o produto de 2 por b e c vezes o Cosseno de A.
Para os ângulos B e C a fórmula é a mesma, apenas alterando seu cosseno e seu lado ao ângulo referido:
Para o ângulo B:
b² = a² + c² - 2.a.c.cos B
Para o ângulo C:
c² = a² + b² - 2.a.b.cos C
Casos dos triângulos acutângulos:
Conhecer e saber identificar nossos lados referentes aos ângulos do triângulo é muito importante para a aplicação dessas medidas nas fórmulas apresentadas acima, pois, sem saber quem são os lados a, b e c, não poderemos substituí-los nas fórmulas da Lei do Cosseno.
Vamos à um exemplo?
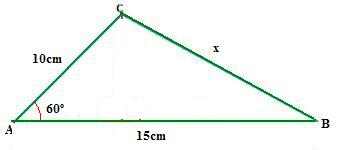
Determine o lado não informado, neste triângulo acutângulo:
Pois bem, analisando o triângulo acima, podemos notar que temos nosso ângulo agudo de 60 graus e que ele é a nossa referência neste exercício, e que também está representado pela letra A.
Vamos agora identificar os lados deste triângulo acutângulo:
Para encontrarmos o lado b, precisamos então saber que este lado está oposto ao seu ângulo referido, no caso, o ângulo B. Para o lado c tomamos com base o mesmo raciocínio, ou seja, ele deve estar oposto ao ângulo C, e finalmente para o lado a, devemos analisar que ele está oposto ao ângulo A.
Depois de analisar os lados deste triângulo acutângulo, teremos encontrado seus lados, veja:

Então concluímos que, o lado c neste triângulo é referente à 15 cm e o lado b é referente à 10 cm.
Se o lado a é igual à x, isso significa que o lado que estamos tentando encontrar é o lado a.
Com isso, podemos aplicar nossos valores obtidos na fórmula da Lei dos Cossenos, utilizando o ângulo A:
Segundo a fórmula:
a² = b² + c² - 2.b.c.cos A
Substituindo os valores na fórmula:
x² = 10² + 15² - 2. 10. 15. cos60°
x² = 100 + 225 - (2. 10. 15). cos60°
x² = 325 - 300.cos60°
Agora verifique na tabela dos arcos notáveis que o cosseno de 60 graus é igual à meio, logo:
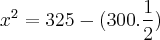
Fazendo o que há dentro do parênteses primeiro teremos:
 que dará:
que dará:  que simplificado dará 150.
que simplificado dará 150.
x² = 325 - 150
x² = 175
x = √175
Simplifique a raiz de 175:
175 | 5
35 | 5
7 | 7
1 5² . 7
√5² . √7 = 5√7
Logo, o lado a deste triângulo acutângulo mede 5√7 cm ou aproximadamente 13,23 cm.
Verificando com o Teorema de Pitágoras, onde: h² = l²+ l²
Que diz: O quadrado da hipotenusa é igual à soma dos quadrados dos lados.
Mas no caso do triângulo acutângulo, o Teorema pode nos dizer também que: h² < l² + l²
Ou seja, o quadrado da Hipotenusa será menor que a soma dos lados ao quadrado.
Se a Hipotenusa é o lado maior do triângulo, então sabemos que a Hipotenusa deste triângulo é o lado c, 15 cm. O quadrado de 15 é igual à 225, logo a soma dos lados ao quadrado desse triângulo, deverá ser maior que 225, vamos ver?
225 < 13,23² + 10²
225 < 175,329 + 100
225 < 275,33
Confere! Logo, o cálculo está correto!
Bem, e no caso de um triângulo obtusângulo?
Casos de triângulos obtusângulos:
Como dito no início da aula, a lei dos Cossenos se aplica à qualquer triângulo, independente de seus ângulos, então essa lei está valendo para o caso do triângulo obtusângulo também.
Então com base disso, vamos direto à um exemplo:
Calcule o lado x do triângulo obtusângulo abaixo:
Note que na tabela dos arcos notáveis, não se tem o cosseno de 120 graus, mas não pense que tudo está perdido! O cosseno de um ângulo obtuso é dado pela seguinte fórmula: cos(ângulo) = -cos(180 - ângulo) e em breve saberemos do porquê do cosseno se tornar negativo e porque subtrair o ângulo desejado por 180, através do círculo trigonométrico:
Mas isso é para a próxima aula, no entanto apenas se atente que: O Cosseno do ângulo referido é igual ao cosseno negativo de 180 pela diferença do ângulo.
Colocando isso em prática temos que:
cos120° = -cos(180°-120°)
cos120° = -cos60°
Agora sim! Verifique na tabela dos arcos notáveis e encontre novamente o cosseno de 60 graus que é meio, só que negativo, lembra? Então:

Vamos então resolver primeiramente essa multiplicação entre - 120 e -1/2 -> Regra dos sinais na multiplicação: Sinal negativo com sinal negativo é igual à sinal positivo, logo, o produto desta multiplicação será positivo:

Então temos:
x² = 136 + 60
x² = 196
x = √196
x = 14
Conclusão: O terceiro lado deste triângulo obtusângulo é de 14 m.
E se tem dúvidas, o Teorema de Pitágoras também nos diz que: Num triângulo obtusângulo, o quadrado da hipotenusa será maior que a soma dos lados ao quadrado -> h² > l² + l²
Se a Hipotenusa é o lado maior do triângulo, podemos dizer que o lado que acabou de ser encontrado -> 14 m é o maior, pois os outros dois lados medem 10 m e 6 m, lados menores que 14 m.
Então o quadrado de 14 que é 196 deve ser maior que a soma do quadrado desses dois lados, será?
196 > 10² + 6²
196 > 100 + 36
196 > 136
Confere, pois 196 é maior que 136!
Vamos à mais outro exemplo?
Encontre o lado y do triângulo obtusângulo abaixo, cujo ângulo obtuso equivale à 120 graus:
.jpg)
Como sempre, vamos identificar o lado que queremos encontrar, e no caso acima, novamente se referindo ao ângulo B, o lado y é o que queremos encontrar, já que está oposto ao ângulo referido.
Nossos outros lados são 7 cm e 5 cm.
Fórmula:
b² = a² + c² - 2.a.c.cos B
Aplicando os valores na fórmula:
y² = 7² + 5² -2.7.5.cos B
y² = 49 + 25 - 70.cos B
y² = 74 - 70.cos120°
Como já visto no exercício anterior, o cosseno de 120° é igual à -1/2:

y² = 74 + 35
y² = 109
y = √109
Logo, nosso terceiro lado deste triângulo obtusângulo é de √109 cm ou aproximadamente 10,45 cm
Verificando com o Teorema de Pitágoras:
10,45 > 7
10,45 > 5
H = 10,45
10,45² =109,203
109,203 > 7² + 5²
109,203 > 49 + 25
109,203 > 74
Confere!
Lembre-se: Nossos valores aplicados à fórmula da lei dos Cossenos são referidos à partir do lado do ângulo apresentado no problema.
Por exemplo, se eu estou me referindo ao ângulo Â, a fórmula usada para a lei dos Cossenos será referente ao ângulo Â, e o mesmo ocorre para os ângulo B e C.
Vamos à um exemplo prático dessa aplicação?
Dados os seguintes elementos de um triângulo ABC: Â = 30º, AB = 8 m,
CB = 5 m. Calcule AC.
Nesse caso, deveríamos desenhar nosso triângulo para visualizarmos melhor os lados a serem inseridos nas fórmulas da lei do cosseno, então, basta desenhar um triângulo qualquer com os de ângulos ABC:
![25 = x² + 64 - 16x. \frac{\sqrt[]{3}}{2}](http://www.ajudamatematica.com/latexrender/pictures/5e947a5e5a5c1d5d881c7f93d31a5b3e.png)
![16x. \frac{\sqrt[]{3}}{2} = 16\frac{\sqrt[]{3x}}{2} = 8 \sqrt[]{3x}](http://www.ajudamatematica.com/latexrender/pictures/4d895f9857849d253471f0d8cd91d9bb.png)




![x = \frac{- b ± \sqrt[]{\Delta}}{2.a}](http://www.ajudamatematica.com/latexrender/pictures/10e488e9904fdadcbcae3024e7faedc9.png)
![x = \frac{- (-13,85) ± \sqrt[]{\335,8225}}{2.1}](http://www.ajudamatematica.com/latexrender/pictures/054da00783942bafff0360d4d63b8dc8.png)













quero uma ajuda
ResponderExcluirEm um triângulo ABC, são dados  = 60°, b = 3√3 e c = 4. Calcule a medida do terceiro lado me ajuda por favor , porque deu 7 , mas se eu fosse dividir , com a raiz , ficaria aproximado a 2, qual estar certo ?
a² = b² + c² - 2.b.c.cos A
Excluira² = (3v3)² + 16 -2*5*1/2
a² = 27 + 16 - 5
a² = 38
a = V38
a = aprox 7.
Creio que neste caso o problema tenha dito que raiz de 3 é apox 1,74 nao?
Excluirok, então eu fiz certo , segui o procedimento que ensinou la em cima
Excluirobrigado.